10119. Перестановка перестановки
n коров
Фермера Джона выстроены в ряд. i-ая корова слева имеет метку i (1 ≤ i ≤ n). Фермер Джон приказал коровам повторить ровно k раз следующий двухшаговый
процесс:
·
Последовательность
коров в позициях a1, …, a2 слева реверсивно меняют свой порядок. Затем
последовательность коров в позициях b1, …, b2 слева реверсивно меняют свой порядок.
Выведите получившийся порядок коров для всех i (1 ≤ i ≤ n) после выполнения этого процесса ровно k раз.
Вход. Первая
строка содержит n (1 ≤ n ≤ 100) и k (1 ≤ k ≤ 109).
Вторая строка содержит a1 и a2 (1 ≤ a1 < a2 ≤ n). Третья строка содержит b1 и b2 (1 ≤ b1 < b2 ≤ n).
Выход. В i-ой строке
выведите метку i-ой коровы
слева после завершения процесса всех обменов.
Пояснение. Изначально порядок коров [1, 2, 3, 4, 5, 6, 7] слева
направо. После первого шага преобразования порядок станет [1, 5, 4, 3, 2, 6, 7].
После второго шага преобразования порядок станет [1, 5, 7, 6, 2, 3, 4].
Повторение обоих шагов второй раз даст ответ.
|
Пример входа |
Пример выхода |
|
7 2 2 5 3 7 |
1 2 4 3 5 7 6 |
РЕШЕНИЕ
моделирование
Анализ алгоритма
Если моделировать процесс перестановки коров, то получим
Time
Limit, так как число повторов двухшагового
процесса k
≤ 109 слишком
велико.
Расставим коров по порядку на позиции от 1 до n.
Для каждой коровы номер i
(1 ≤ i ≤ n) найдем
позицию, в которой она окажется через k итераций. Для каждой коровы найдем
число итераций p, через которое она снова
будет занимать исходное место. Это число p ≤ n ≤ 100 не велико. Тогда
эта корова займет исходное место через 2p, 3p, 4p … итераций.
Через k – (k % p)
итераций рассматриваемая корова снова
окажется на своем исходном месте (так как указанное число делится на p). Остается совершить еще k % p итераций
чтобы найти конечное положение коровы.
Пример
Изначальный порядок коров имеет вид:
![]()
Шаг 1

Шаг 2
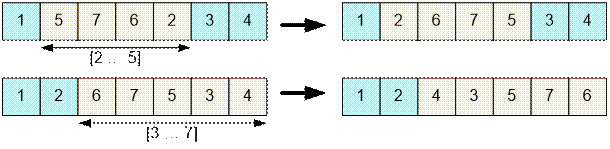
Реализация алгоритма
Объявим
массив pos. Если корова
номер i после k итераций займет позицию cur, то присвоим pos[cur] = i.
int pos[101];
Пусть некоторая корова
находится в позиции x. Функция nex(x) возвращает
позицию этой коровы после двухшагового процесса. Если корова находится в позиции
x, которая принадлежит отрезку [a1; a2], то после его переворачивания корова переместится в позицию
a1 + a2 – x.
int nex(int x)
{
if (a1 <= x && x <= a2) x = a1 + a2 - x;
if (b1 <= x && x <= b2) x = b1 + b2 - x;
return x;
}
Основная часть
программы. Читаем входные данные.
scanf("%d %d", &n, &k);
scanf("%d %d", &a1, &a2);
scanf("%d %d", &b1, &b2);
Для каждой коровы
номер i находим ее положение после
выполнения процесса всех обменов.
for (i = 1; i <= n; i++)
{
В переменной p находим количество итераций (одна итерация есть выполнение
двухшагового процесса один раз), через которое i-ая корова снова окажется на своем месте. Переменная cur содержит текущую позицию коровы.
p = 1; cur = nex(i);
Выполняем цикл пока i-ая корова не станет на свое начальное место – позицию
номер i.
while (cur != i)
{
p++;
cur = nex(cur);
}
Через k – (k % p) итераций
i-ая корова снова окажется на i-ом месте. Проведем еще k % p итераций
для нахождения финального месторасположения i-ой коровы.
kk = k % p;
for (j = 0; j <
kk; j++)
cur = nex(cur);
Корова номер i после k
итераций займет позицию cur.
pos[cur] = i;
}
Выводим конечное
расположение коров после завершения всех обменов.
for (i = 1; i <= n; i++)
printf("%d\n", pos[i]);
Реализация алгоритма – Time Limit
В случае
непосредственного моделирования операций из-за ограничения k ≤ 109 получаем Time Limit.
#include <cstdio>
#include <algorithm>
using namespace std;
int i, n, k, a1, a2, b1, b2;
int m[101];
int main(void)
{
scanf("%d
%d", &n, &k);
scanf("%d
%d", &a1, &a2);
scanf("%d
%d", &b1, &b2);
for (i = 1; i <=
n; i++)
m[i] = i;
for (i = 0; i <
k; i++)
{
reverse(m + a1, m + a2 +
1);
reverse(m + b1, m + b2 +
1);
}
for (i = 1; i <=
n; i++)
printf("%d\n", m[i]);
return 0;
}